TEORI BAHASA DAN AUTOMATA
Finite State Automata
Materi yang akan kita bahasa adalah :
1. Penerapan FSA (Finite State Automata)
2. Penerapan DFA (Deterministic Finite Automata)
3. Penerapan NFA (Nonfeterministic Finite Automata)
4. Ekuivalen antar DFA
5. Reduksi Jumlah State
Pembahasannya :
1. Penerapan FSA (Finite State Automata)
Finite State Automata atau automata berhingga state, selanjutnya disebut sebagai FSA yaitu suatu model matematika dari suatu sistem yang menerima input dan ouput diskrit. FSA merupakan mesin automta dari bahas regular, suatu FSA memiliki state yang banyaknya berhingga dan dapat berpindah-pindah dari suatu state ke state lain. Perubahan state ini dinyatakan oleh fungsi transisi. FSA tidak memiliki tempat penyimpanan, sehingga kemampuan 'mengingatnya' terbatas, hanya bisa mengingat state yang terkini. Contoh FSA antara lain elevator, text editor, analisa leksikal, protocol komunikasi jaringan dan pencek parity. FSA berdasar pada pendefinisian kemampuan berubah state-statenya bisa dibagi menjadi Deterministic Finite Automata (DFA) dan Non-deterministic Finite Automata (NFA).
Secara formal FSA dinyatakan oleh 5 tupel atau M = (Q, Σ, δ, S, F)
Q = himpunan state atau kedudukanΣ = himpunan simbol input atau masukan atau abjad
δ = fungsi transisi
S = state awal atau kedudukan awal (initial state), S є Q
F = himpunan state akhir, F ∩ Q (jumlah state akhir pada suatu FSA bisa lebih dari satu)
FSA juga terbagi menjadi dua jenis, yaitu :
- DFA (Deterministic Finite Automata)
Artinya : Dari suatu state bisa terdapat 0, 1 atau lebih busur keluar (transisi) berlabel simbol input yang sama
2. Penerapan DFA (Deterministic Finite Automata)
Deterministic Finite Automata atau automata berhingga determistik, selanjutnya disebut sebagai DFA. Pada DFA, dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima. Suatu string x diyatakan diterima bila δ(S, x) berada pada state akhir atau final state.
Contoh :
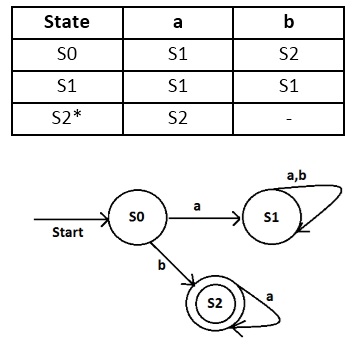
3. Penerapan NFA (Nondeterministic Finite Automata)
Non-deterministic Finite Automata, selanjutnya disebut sebagai NFA. Pada NFA, dari suatu state bisa terdapat 0 atau 1 atau lebih busur keluar (transisi) berlabel symbol input yang sama. Suatu string diterima oleh NFA bila terdapat suatu urutan transisi sehubungan dengan input string tersebut dari state awal menuju state akhir. Untuk NFA, maka harus mencoba semua kemungkinan yang ada sampai terdapat satu yang mencapai state akhir.
- NFA mempunyai fungsi transisi yang menetapkan nol atau lebih state untuk sebuah symbol input
- NFA menerima String, jika hasil akhir penelusuran string berakhir di salah satu final state
- String akan diterima apabila ada suatu path bervariasi w dari state ke salah satu final state, maka w akan diterima
Contoh :

Berdasarkan contoh Deterministic Finite Automata (DFA) dan Non Deterministic Finite Automata (NFA) yang ada di atas, terlibat perbedaan antara DFA dan NFA yaitu :
- Pada Deterministic Finite Automata, jika suatu state diberi inputan maka state tersebut akan selalu tepat menuju satu state
- PADA Non Deterministic Finite Automata, jika suatu state diberi inputan maka mungkin saja bisa menuju ke beberapa state berikutnya. Dapat dilihat di S0, jika diberi inputan b bisa menuju ke S1 dan S2
4. Ekuivalen antar DFA

Hubungan antara DFA, NFA dan Ekspresi Regular
Dua DFA M1 dan M2 diyatakan ekuivalen apabila L (M1) = L (M2)

5. Reduksi Jumlah State
Untuk suatu bahasa regular, kemungkinan ada sejumlah Deterministic Finite Automata yang dapat menerimanya. Perbedaannya hanyalah jumlah state yang dimiliki atumata saling ekuivalen tersebut. Tentu saja, dengan alasan kepraktisan, kita memilih automata dengan jumlah state yang lebih sedikit.
Sasaran kita disini adalah mengurangi jumlah state dari suatu Finite State Automata, dengan tidak mengurangi kemampuannya semula untuk menerima suatu bahasa.
Ada dua buah istilah baru yang perlu kita ketahui yaitu :
- Distinguishable yang berarti dapat dibedakn
- Indistinguishable yang berarti tidak dapat dibedakan
Redaksi Jumlah State pada FSA :
- Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semulah.
- State pada FSA dapat direduksi apabila terdapat useless state
- Hasil FSA yang direduksi merupakan ekuivalen dari FSA semula
Keterangan :
Useless state adalah state yang tidak menerima inputan dari manapun tetapi mengeluarkan output
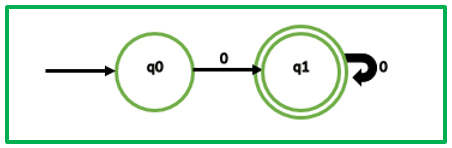
Pembahasan :
(q0, q1)
q0,0 → q1 & q1,0 → q1 →q1,q1 → indistinguisable, sehingga dapat direduksi
Contoh soal :
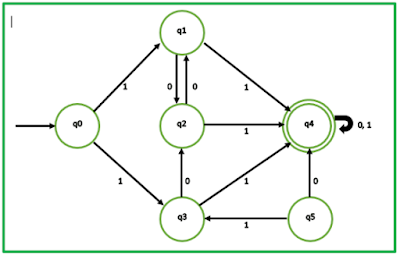
Penyelesaian :
Didapat State yang tidak useless : q0, q1, q2, q3, q4
- q0, q1 → distinguisable
- q0, q2 → distinguisable
- q0, q3 → distinguisable
- q0, q4 → distinguisable
- q1, q2 → distinguisable
- q1, q3 → distinguisable
- q1, q4 → distinguisable
- q2, q3 → distinguisable
- q2, q4 → distinguisable
- q3, q4→ distinguisable
Pembuktian :
(q0, q1)
q0, 0 → q1 & q1, 0 → q2 => q1, q2
q0, 1 → q3 & q1, 1 → q4 => q3, q4 = distinguisable
(q0, q2)
q0, 0 → q1 & q2, 0 → q1 => q1, q1
q0, 1 → q3 & q2, 1 → q4 => q3, q4 = distinguisable
(q0, q3)
q0, 0 → q1 & q3, 0 → q1 => q1, q1
q0, 1 → q3 & q3, 1 → q4 => q3, q4 = distinguisable
(q1, q3)
q1, 0 → q2 & q3, 0 → q2 => q2, q2
q1, 1 → q4 & q3, 1 → q4 => q4, q4 = distinguisable
(q1, q2)
q1, 0 → q2 & q2, 0 → q1 => q1, q2
q0, 1 → q4 & q2, 1 → q4 => q4, q4 = distinguisable
(q2, q3)
q2, 0 → q1 & q3, 0 → q2 => q1, q2
q2, 1 → q4 & q3, 1 → q4 => q4, q4 = distinguisable
Maka dapat direduksi menjadi :

Terimakasih, semoga dapat bermanfaat. Mohon maaf apabila ada kesalahan kata dalam penulisan, jika ada kesalahan silahkan tulis di kolom komentar.
Daftar Pustaka
- Materi 7 Perkuliahan "Finite State Automata & Non Finite State Automata" Dosen pengampu Teori Bahasa dan Automata : Garno, M,Kom. Fakultas Ilmu Komputer Universitas Singaperbangsa Karawang
- Materi 7 Perkuliahan "Finite State Automata & Non Finite State Automata" Dosen pengampu Teori Bahasa dan Automata : Garno, M,Kom. Fakultas Ilmu Komputer Universitas Singaperbangsa Karawang


Komentar
Posting Komentar